1.     Preface

Today I would like to write a brief description of an exercise I got from my Prof nine years ago during the first semester of my studies. For me as a total greenhorn to programming, this exercise was far beyond my limits. But nine years later, during last winter holidays I felt the ambition to try this exercise again.

The exercise is: Writing an algorithm that solves a sudoku.
Although I know that there a hundreds of thousands of algorithms out there, that are doing this job quite well and presumably much more efficient  and reliable than my algorithm does, it is a strong desire for me to share my solution to the world. For this purpose, I am using my blog which I normally use to write about German politics (also in German language).
Firstly I have to admit that my algorithm requires a large heap to handle difficult sudokus. If the heap is to small the algorithm will end up in a stackoverflowerror for complex sudokus.

You can find the code on my github repository: https://github.com/StefanMemmel/sudoku_solver

The repository contains two classes:

The class App.java realises a command-line application to enter a sudoku line by line. The class Sudoku.java provides the actual algorithm to solve the sudoku. I’ll freely admit that I have neither solved a Sudoku for myself (I am to inpatient for that) nor read any literature on how to do this. The algorithm I implemented is probably some sort of backtracking algorithm. That means it tries to find a solution recursive, which can lead to a stackoverflowerror if the sudoku is very complex and the heap size of the Java Virtual Machine is to small.

2.    The idea of my algorithm

So let`s get right into it:

The basic idea of my algorithm is to fill the first blank with the lowest valid digit and then go to the next blank and fill this blank with the lowest possible digit as well. If a blank could not be filled with any digit, the algorithm goes back to the last blank and refills this blank with the second lowest possible digit, if that is also not possible it goes back to the second to last blank and so on.

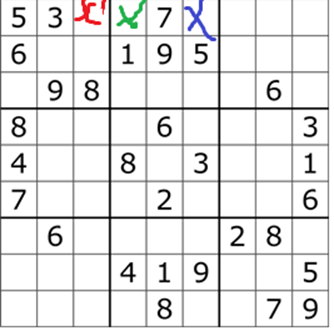
In figure 1 the algorithm will find the first blank where the red cross is. Because there is neither a digit ‘1’ in the first row nor in the third column nor in the left-top block, the algorithm will fill this blank with the digit ‘1’ and go to the next blank, which is marked with the green cross.

In the blank with the green cross the digit ‘2’ fits. For the blank with the blue cross the ‘4’ is the lowest possible digit.

If you have a look at the third row, you may notice that filling the green and the blue blank with the digits ‘2’ and ‘4’ can not lead to the final solution, because the block also needs the digit ‘8’, which can not be placed in one of the remaining blanks of the block in the third row, because there is already a digit ‘8’ in the third row (left 3×3 – block). So the algorithm has to go back and refill the preceding blanks with other digits (the second lowest possible digit or speaking in general the next possible lowest digit).

As you may have noticed so far, we need a recursive structure to fit this task, but we also need a dynamic object to save all the blanks we have filled.

This job is done by the ArrayList<int[]> freeCells.

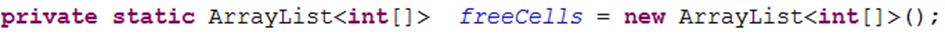
Before discussing the function solve(int[][] matrix, int startDigit) which realizes the core of the algorithm, I want to introduce a couple of auxiliary functions that have been implemented to make the code a little bit smarter and easier to understand.

3.     Auxiliary functions

3.1. static int[][] get3Block(int[][] matrix, int row, int column)

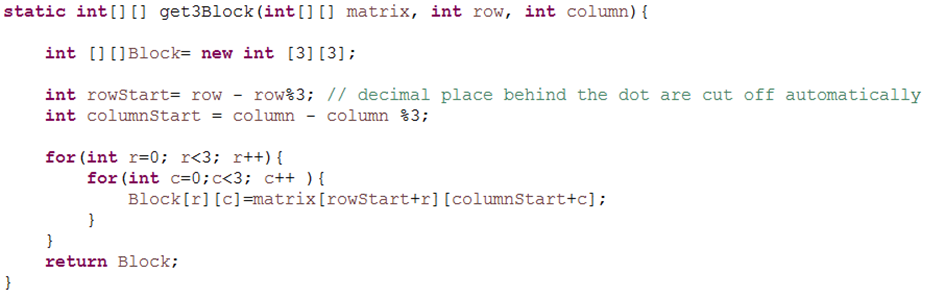
Figure 3 shows the function static int [][] get3Block( int [][] matrix, int row, int column), that is used to extract the 3×3 – block, where a given cell (with the coordinates row and column) belongs to. So you have to call this function with the whole sudoku (first value) and the coordinates for the cell, which block should be extracted, to get that block in return.

3.2. static int getNumberFromBlock(int[][] matrix, int startDigit)

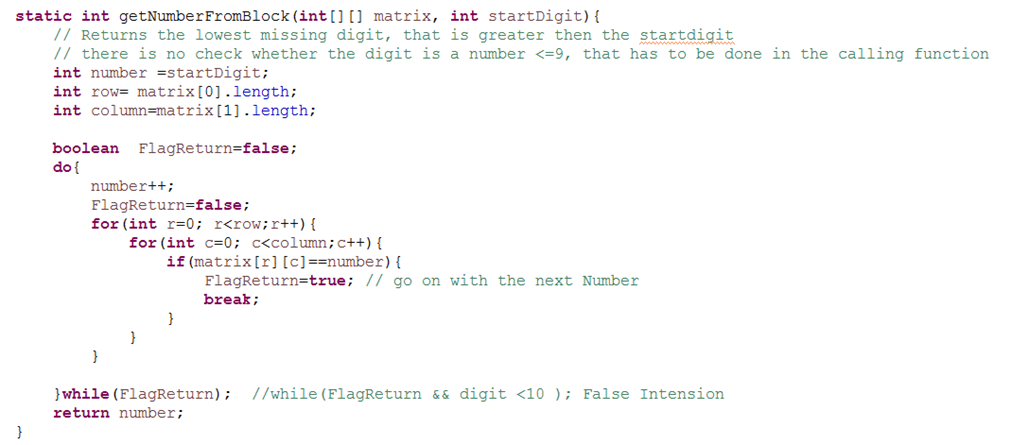
The next function getNumberFromBlock(int[][] matrix, int startDigit) iterates through a given integer matrix and returns the lowest positive number, which is greater than the start digit and not contained in the block.

E.g. the matrix should be m=[0,2,1,0,4,5,0] (There is no restriction to 3×3 matrixes for this function);

So. if the startDigit is ‘1’ or ‘2’ the function will return 3, if the startDigit is ‘3’, ‘4’ or ‘5’ it will return 6. You may notice that the two auxiliary functions in Figure 3 and Figure 4 will be used later to get the lowest possible digit for a sudoku block.

3.3. static boolean rowAndColumnUnique(int[][] matrix, int r, int c)

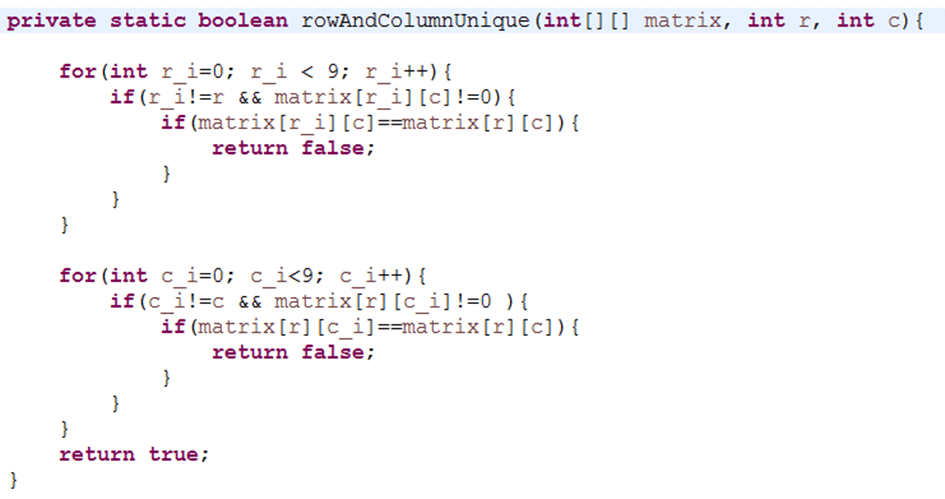
The challenge of solving a sudoku is not only that the digits must occur only once in the 3×3-block, but that they also have to be unique in each row and column where they stand. Checking this reqirement is the job of the boolean function rowAndColumnUnique(int[][] matrix, int r, int c), which you can see in figure 5. The function is called with a two-dimensional integer matrix and the coordinates of a specific cell from that matrix. The function returns true if the value of that specified cell is unique in the dedicated row and column, otherwise false.

3.4. static int[] findFirstZero(int[][] matrix)

Last but not least the function findFirstZero(int[][] matrix) returns the blanks in the sudoku. Per definition the blanks are cells that have the integer value = 0. The function starts the search for the first blank left hand at the top and returns the coordinates of that blank as int[2] matrix. If there are no more blanks in the sudoku it returns [-1,-1].

4.     The core algorithm

Now as I have explained all necessary auxiliary functions I will show you the function solve(int[][] matrix, int startDigit), that implements the core of my algorithm:

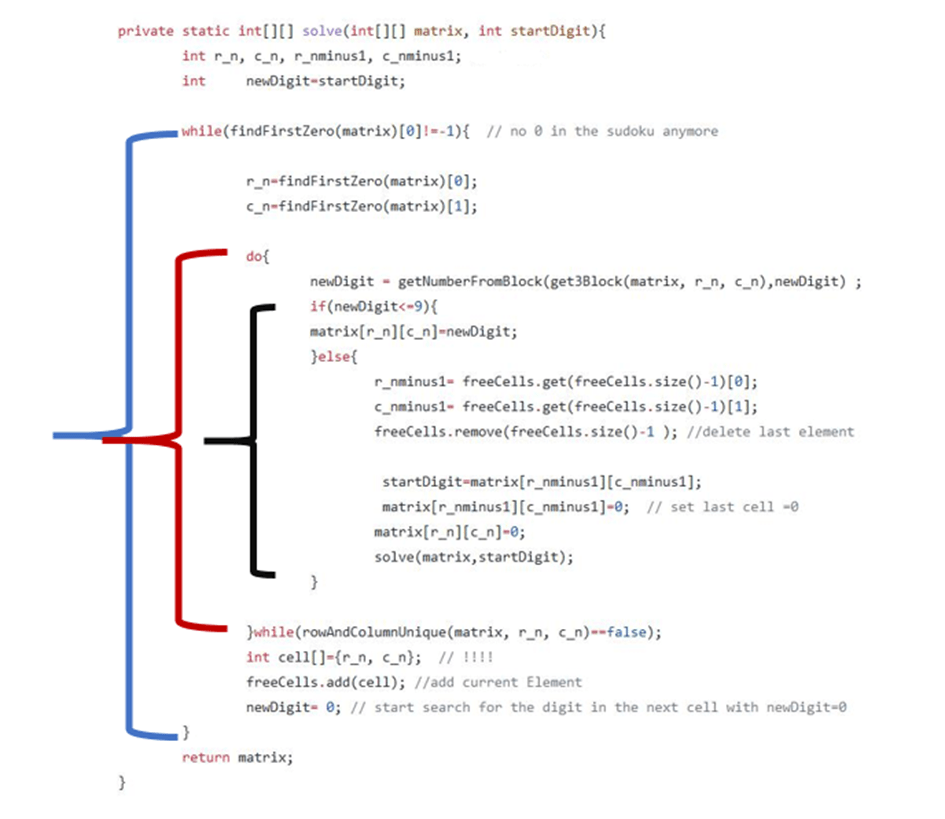
The function solve(int[][] matrix, int startDigit), which is the core of my algorithm, consists of three nested control structures that I have marked in figure 7 with coloured brackets. The first structure (blue bracket) is a while – loop, iterating over the blanks. It stops, when the last blank is filled and the function findFirstZero(int[][] matrix) returns [-1, -1]. (c.f. paragraph 3.1)

In the loop that iterates over the blanks, there is another loop (red bracket) that tries to find valid digits for those blanks. The possible digits for a current blank (with the coordinates r_n, c_n) are returned by the function getNumberFromBlock(int[][] matrix, int startDigit). (c.f. paragraph 3.2) If the returned digit is not unique at its row and its column, the function getNumberFromBlock(…) will be called once again, with a higher startDigit as parameter. Otherwise the loop breaks.

The function getNumberFromBlock(…) is not restricted, to the range of the digits from 1 to 9, it can also return 10. This is the case, when all the digits returned before, ere not unique in the column or the row (breaking condition of the inner loop).

To handle this phenomenon there is an if-else condition (black bracket). If the newDigit is less or equal than nine, everything is fine and the blank can be filled with these digit. If not (else – branch) the blank that was handled before has to be refilled with a higher digit. To do this, the coordinates of the preceding blank are read from the ArrayList<int[]> freeCells. The value that was filled in that blank is extracted from the matrix and written to the variable startDigit. Then the cell is set to zero.

Now the function solve(int[][] matrix, int startDigit), is called with a higher startDigit recursively to fill the previous blanks. As I mentioned before the algorithm may end in a stackoverflowerror if the sudoku is to complicate. Of course, I´d like to fix this error as soon as I have the time for that (probably in my next holidays). 

As a temporary solution I have added a try-catch block to the recursive call in the else – branch.

In some cases, the algorithm may also be helpful with sudokus that are actual to complex for it. E.g. the sudokus in figure 1 could not be solved by the algorithm (at least on my computer). But it is relatively easy to see that only the digit ‘5’ could fit in the cell at the centre of that sudoku, and if you see that, you will see that the digit left in the middle column are ‘3’ and ‘4’. Because the block at the bottom still contains a digit ‘4’ this digit must go in the middle column to the block at the top (3rd row). So, you get a sudoku that could be solved:

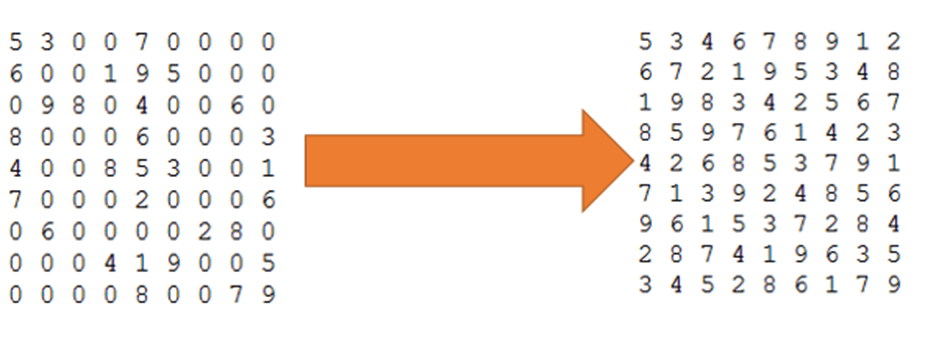
Figure 9 shows the solution of the example in figure 1. So, you see, that with a little “human – help” the algorithm could also find a solution for this example.

5.    Future prospects

An algorithm that works only in a few numbers of cases is obviously inconvenient. One possible solution addressing this problem is of course to maximize heap size. A finer solution will be reducing recursive calls.
Possibly this can be done, by going back not to the last blank, but to the last blank in the same 3×3 block. For this approach the concept of saving the blanks has to be changed. The simple ArrayList<int[]> freeCells, witch stores the coordinates (c.f. paragraph 2) won’t be sufficient anymore. This task requires not only a lot of brainpower but also a complete redesign of the function solve(int[][] matrix, int startDigit), so I decided to postpone that to a later release.

So all in all my algorithm is far from perfect, but at least I hope you get an idea, how the task of solving a sudoku could be handled and what auxiliary functions may be useful for that.